本篇文章仅有题解,若要查看题目请访问
建模整理
给定一个n行m列矩阵,选取r条行、c条列,将行列重合部分组成一个r行c列的子矩阵,并规定:
相邻的元素:矩阵中的某个元素与其上下左右四个元素(如果存在的话)是相邻的。
矩阵的分值:矩阵中每一对相邻元素之差的绝对值之和。
本体任务即为:从这个矩阵中选出一个r行c列的子矩阵,使得这个子矩阵的分值最小,并输出这个分值。
解题思路
算法选取
暴力算法,该算法只能过50%的数据,往上的测试点T掉
→ 贪心,搞不出来,好像也没人搞出来
→ 记搜+剪枝,据说可以AC,但是个人比较菜,不会
→ 只剩DP了
—>题解里有大佬用状压?反正我不会
状态
之前在分析暴力算法的时候,发现暴力中既要搜行,又要搜列。那么,有没有想过,能不能只搜列、不搜行呢?很明显,行的计算只能通过记忆化搜索或者动态规划实现。这里就只说动态规划,记忆化搜索就不再赘述了。既然是DP,就有一个状态,因为这里是DP行,所以我们假设状态的含义为:
dp[i]:前i行(包括第i行)的最优解
由于题目有一个最多只能取r行的限定,所以状态应转化一下:
dp[i][j]:i行取j行(包括第i行)的最优解
克服了第一个难关,继续加油!
状态转移方程
当前是第i行取j行,那前一次取是第几行呢?我们不妨用k来表示。当前是取j行,那前一次自然就是取j-1行了。有了前一次,那么前一次如何变到当前状态?很明显,就是加上第k行和第i行 列相减 的绝对值,以及第i行内部相减的绝对值
这个时候,状态转移方程变自然推出了:
dp[i][j] = min(dp[k][j-1] + sumc(k, i) + sumv(i))
PS: sumc函数表示 第k行和第i行 列相减 的绝对值
sumv函数表示第i行内部相减的绝对值
克服了第二个难关,胜利在望!
边界
由于无论取哪些列,只要是只取1行的情况,必然dp[i][1]只有第i行内部相减的绝对值,像下面这样:
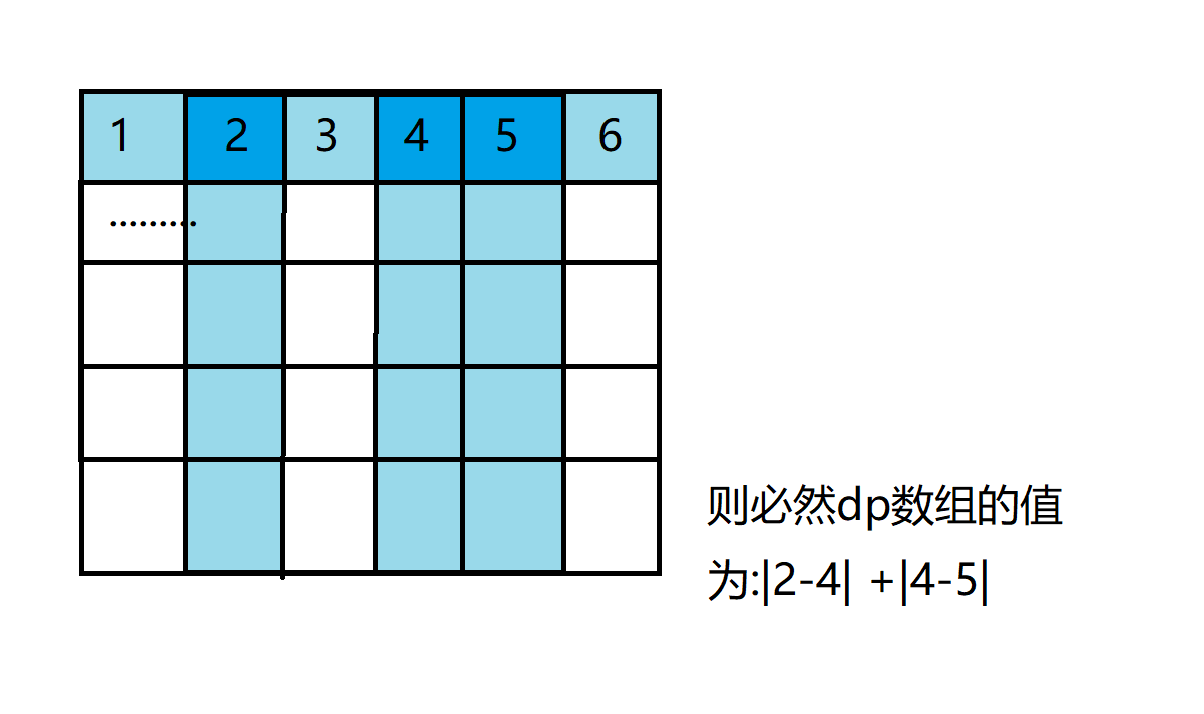
大功告成,只剩肝代码!
代码实现
代码细节就不多说了,重在上面DP的理解
